| |
| |
|
|
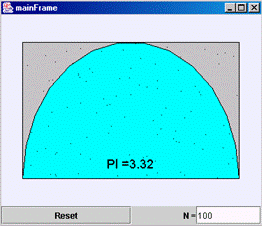
Fig.
7.7: View of the virtual-lab. |
|
|
|
| |
|
| System
description |
| |
| The
goal of this virtual-lab is to estimate the value of PI using a Monte Carlo
method. The method is as follows: |
| |
Suppose
that we are throwing a dart over a square surface of side 2 m. There is
a circle of radius 1 m. inscribed in the square. Assuming that the probability
is uniformly distributed, the probability of hitting inside the circle
is equal to PI/4. Dividing the number of hits by the number of throws,
it is obtained an approximation of PI. |
| |
| The
larger the number of throws is, the better the estimation is. This virtual-lab
allows the user to select the number of throws and provides the corresponding
estimation of the PI value. |
|
|
| Introduction |
| |
| The
introduction of the virtual-lab is shown in Fig. 7.33. |
| |
|
Fig.
7.33: Introduction. |
|
|
| Model |
| |
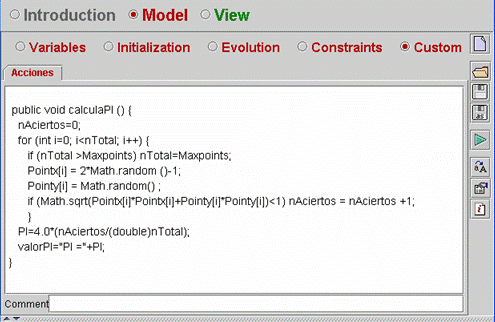
| The
Java method that estimates PI has been defined in the Custom panel (see
Fig 7.34). The coordinates of the throws are stored in the arrays Pointx
and Pointy.When
the user changes the number of throws, this method is executed: a new set
of throws is generated and a new estimation of PI is obtained. Every estimation
of PI uses a different seed and, consequently, a different sequence of random
variates. |
| |
|
Fig.
7.34: Method to estimate the value of PI. |
|
|
| View |
| |
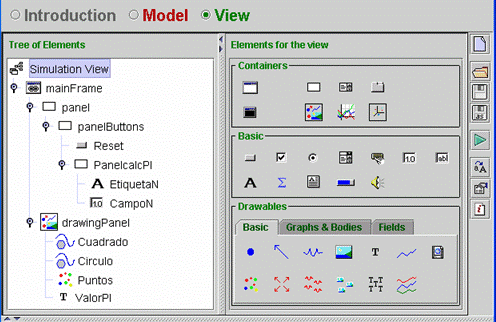
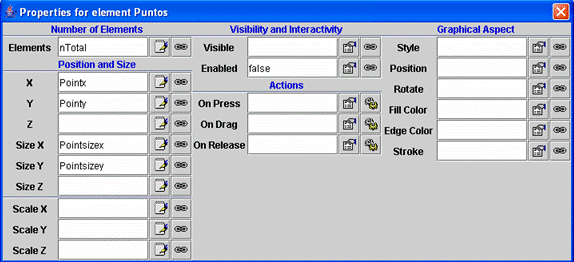
| The
tree of elements is shown in Fig. 7.35. The properties of the Puntos
element (i.e., the set of points representing the throws) is shown in Fig.
7.36. |
| |
|
Fig.
7.35: Tree of elements. |
| |
|
Fig.
7.36: Properties of the set of points representing the throws. |
| |
|